Vector Quantization in Python with Example – Learn How it Works

Introduction to Vector Quantizer: Learning Vector Quantization, often known as LVQ. It  is a type of Artificial Neural Network that draws inspiration from biological neural network models. It is built on a supervised learning prototype classification algorithm, and it trained its network using a self-organizing map-like competitive learning algorithm. The multiclass classification issue can also be resolved by it. There are two layers in LVQ: the input layer and the output layer. Following is a description of the Learning Vector Quantization’s architecture using n input features and n classes for any sample.

Consider an input dataset of size (a, b), where a is the number of training examples and b is the number of features in each sample, and a label vector of size ( a, 1 ). Prior to discarding any training samples, it initializes the weights of size (b, c) from the first c training examples with various labels. The number of classes in this instance is c. Following each training example, the successful vector (the weight vector with the smallest distance, for instance, the Euclidean distance from the training example) is updated whereas the remaining input data are iterated over. The rule to update the weights is:

if correctly_classified:

   

else:

   

where the winning vector is denoted by n, the mth feature of the training example is denoted by m and the lth training example from the input data is denoted by l. where k is the learning rate at time t. New instances are classified using trained weights after the LVQ network has been trained. The winning vector’s class is assigned to a brand-new example.

Also Read: Top 10 Typical Applications of NLP (Natural Language Preprocessing)

Vector Quantization Algorithm

In this section, we will learn about the vector quantization algorithm.

Vector Quantization Example

Let’s examine the underlying mathematical idea of LVQ. Take into account the target class and the next five input vectors.

Vector	Class Label
[0 0 1 1]	1
[1 1 1 1]	2
[0 0 0 1]	2
[1 0 0 1]	1
0  1 1 0]	1

There are two target classes and four input components (x1, x2, x3, x4) in each input vector (1, 2). Let’s distribute the weights according to the class. The first two vectors can be used as weight vectors because there are two target classes: w1 = [0 0 1 1] & w2 = [1 0 0 0].

It is possible to train using the final three vectors. Consider 0.1 as the learning rate. Taking our initial data point (the third vector).  Let vector be [0 0 0 1] and target class be 2. The Euclidean distance must be calculated next. The equation is:

where Weight is w_ij. The original input component is x_i. Now that we know how far the input unit is from the initial and 2nd weight vectors, respectively, we can compute D(1) and D(2).

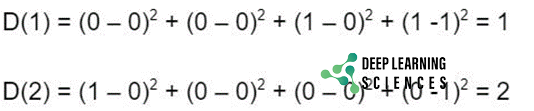
Now that we have the input unit’s distance from the first and second weight vectors, respectively, we can calculate D(1) and D(2). As D(1) is less than D(2) so D(1) will be selected at j=1. It should be the same as the target class otherwise the weights need to be updated.

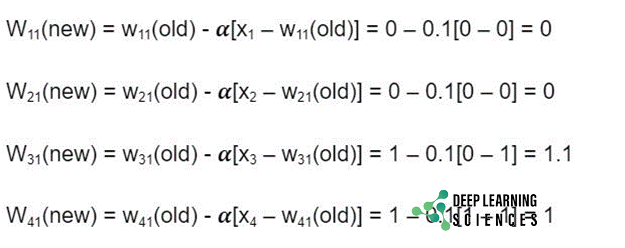
The updated weight produced as:

This process will be repeated for all input vectors.

Vector Quantization Using Python

We need a few steps for the implementation of vector quantization.

We will use the digits dataset available in sklearn.

from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import minmax_scale
from sklearn.metrics import precision_score, recall_score, accuracy_score, f1_score
import matplotlib.pyplot as plt
import numpy as np
import math
dig = datasets.load_digits()
print(dig)
A = dig.data
B = dig.target

a_train, a_test, b_train, b_test = train_test_split(A, B, shuffle=False, test_size=0.3)
def lvq_train(A, y, a, b, mx_ep, mn_a, e):
    c, train_idx = np.unique(y, True)
    r = c
    W = A[train_idx].astype(np.float64)
    train = np.array([e for i, e in enumerate(zip(A, y)) if i not in train_idx])
    A = train[:, 0]
    y = train[:, 1]
    ep = 0
    while ep < mx_ep and a > mn_a:
        for i, x in enumerate(A):
            d = [math.sqrt(sum((w - x) ** 2)) for w in W]
            mn_1 = np.argmin(d)
 
            mn_2 = 0
            dc = float(np.amin(d))
            dr = 0
            mn_2 = d.index(sorted(d)[1])
            dr = float(d[mn_2])
            if c[mn_1] == y[i] and c[mn_1] != r[mn_2]:
                W[mn_1] = W[mn_1] + a * (x - W[mn_1])
 
            elif c[mn_1] != r[mn_2] and y[i] == r[mn_2]:
                if dc != 0 and dr != 0:
 
                    if min((dc/dr),(dr/dc)) > (1-e) / (1+e):
                        W[mn_1] = W[mn_1] - a * (x - W[mn_1])
                        W[mn_2] = W[mn_2] + a * (x - W[mn_2])
            elif c[mn_1] == r[mn_2] and y[i] == r[mn_2]:
                W[mn_1] = W[mn_1] + e * a * (x - W[mn_1])
                W[mn_2] = W[mn_2] + e * a * (x- W[mn_2])
        a = a * b
        ep += 1
    return W, c
def lvq_test(x, W):
    
    W, c = W
    d = [math.sqrt(sum((w - x) ** 2)) for w in W]
 
    return c[np.argmin(d)]
W = lvq_train(a_train, b_train, 0.2, 0.5, 100, 0.001, 0.3)
print(W)

predicted = []
for i in a_test:
    predicted.append(lvq_test(i, W))
    
def print_metrics(labels, preds):
    print("Precision Score: {}".format(precision_score(labels,
           preds, average = 'weighted')))
    print("Recall Score: {}".format(recall_score(labels, preds,
           average = 'weighted')))
    print("Accuracy Score: {}".format(accuracy_score(labels,
           preds)))
    print("F1 Score: {}".format(f1_score(labels, preds, average =
           'weighted')))
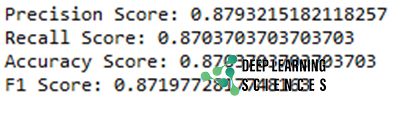
print_metrics(b_test, predicted)

The final output will look like this:

Vector Quantization in Machine Learning

Machine learning typically uses vector quantization for categorization problems. Here, quantization enters the picture as a method to both maximize performance accuracy and minimize the size of the neural network. This is especially important for on-device apps because memory and processing power are always limited. Quantization is a method used in deep learning to approximate a neural network that uses floating-point values with a neural network with low bit width numbers. As a result, using neural networks uses far less memory and is computationally much less expensive.

FAQs