Batch Normalization is the process of normalization that involves shifting the value of the sample variance in the data to a common scale without distorting contrasts in the value range. The batch normalization technique normalized each input passed to the layers in the neural network. As a result, learning is controlled, and sophisticated neural networks can be trained using a significantly smaller number of training epochs.

Batch Normalization’s need during the training of the model
Creating a deep neural network with several layers is necessary for deep learning since these networks might be sensitive to the learning algorithm’s architecture and underlying initial random weights. One possible cause of this issue is that when the parameters are refreshed after each mini-batch, the dispersion of the data to layer upon layer below in the network may shift. This can force the learning system to seek a moving target continuously. Internal covariate shift is used to refer to this adjustment in the input distribution to network layers.
The difficulty lies in the fact that the model is updated layer-by-layer backward from the input to the output while using an approximate error that assumes the parameters in the layers before the current layer is constant.
A rich approach to parametrizing virtually any deep network is provided by batch normalization. Reparameterization significantly lessens the problem of updating plans over many levels. The data distribution is also maintained via batch normalization. One of the key features we include in our model is batch normalization. It acts as a regularizer, normalizing the inputs throughout the back-propagation algorithm process, and can be used in most models to improve convergence.
How Batch Normalization Works
Batch normalization normalizes a layer input by subtracting the mini-batch average value. Then it divides it by the standard deviation. Each epoch in a single batch receives a mini-batch or a portion of the entire training data. This is the formula of working.
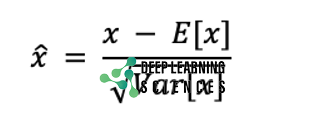
In the above formula, ̂x is a normalized vector. The problem of internal covariate shift is resolved, and regularization is provided, by normalization, which guarantees that the data have an average of 0 and a deviation of 1. It means that the input distribution to every neuron will be the same.
However, the network’s capacity for representation has been seriously diminished. As there are some non-linear relationships that are lost during normalization, each layer’s weight changes and data noise are partially eliminated if the layers are normalized. As a result, less-than-ideal weights may be transmitted.
Batch normalization corrects this by including the gamma and beta trainable parameters, which can scale and move the normalized output.

To identify the best distribution that takes into consideration the sparseness of the weight changes and the noise in the data, stochastic gradient descent can tweak the parameters and during standard backpropagation. The normalized input distribution is essentially scaled and shifted by these parameters to fit the quirks of the given dataset. For instance, if the best input distribution for a dataset is unnormalized, then and will converge to Var[x] and E[x] and the original unnormalized x vector will be returned. As a result, batch normalization makes sure that the normalization is always the suitable for the considered dataset in question.
Benefits, Formula and Applications of Batch Normalization
There are many advantages of batch normalization which are given below.
- Speedy Training: The Batch normalization expedites training by normalizing the hidden layer activation.
- Better handling of internal covariate: It fixes the internal covariate shift issue. By doing this, we make sure that each layer’s input is distributed with a standard deviation and mean that are similar. These neurons’ learning capabilities are highly constrained since they must constantly adapt to the shifting input distribution. Internal covariate shift refers to this input distribution that is always shifting.
- Regularize the loss function: The loss function is smoothed using batch normalization, which increases the model’s training efficiency by improving the model’s parameters.
- Handles vanishing and exploding gradients: Batch normalization also addresses the problem of vanishing or expanding gradients. Saturated activation functions were employed prior to Rectified Linear Units (ReLUs). A saturated function, like the sigmoid function, has a “flattened” curve near the left and right boundaries.
Also Read: Reinforcement Learning Applications and Working
The gradient in the sigmoid function moves closer to 0 as the value of x moves in the direction of. Weights can be moved toward the saturated ends of the sigmoid curve as a neural network is trained. As a result, the gradient decreases until it is almost zero. When multiplied together further into the network, even modest gradients become even more negligible. The gradient approaches zero exponentially more frequently when backpropagation is used. Network depth is significantly constrained by this “vanishing” gradient. Although this vanishing gradient may be readily managed by using a non-saturated activation function like ReLU, batch normalization still has a place because it stops the parameters from being pushed to those saturated regions by making sure no value has gone too high or low in the first place.
Conclusion
In this article, we learned what batch normalization is and how it enhances neural network performance. However, we don’t have to do all of this by ourselves because deep learning tools like PyTorch and TensorFlow handle the implementation’s complexity. Being a data scientist, it is still important to comprehend the complexities of the back end.
FAQs
Why does batch normalization speed up training?
Additionally, deeper networks require more iterations due to the lower gradients seen during backpropagation. We can use considerably greater learning rates when using batch normalization, which accelerates the training of networks even more.
Do the results of batch normalization become better?
Applying batch normalization to the neurons before using an activation function in practice results in greater performance. In other words, if we use the neurons of a layer as input values for an activation function, we get the same outcome for the activations themselves if we make them zero-centered with a variance of one.