The human eye function is a unique visual system. Humans have a primary visual cortex, also known as V1, containing 140 million neurons, with tens of billions of connections between them, that’s not just it, a human eye has v2,v3,v4&v5 which process images excellently. It won’t be wrong if we call it a supercomputer that is superbly adapted to understand the visual world. As easy as it seems to recognize handwritten digits isn’t easy. Humans are tremendously good at making sense of what our eyes show us, that too unconsciously.
We’ll understand the complexity when we work on a computer program to recognize an image. For example, we are recognizing a digit using a program and we’ll notice that “a 9 has a loop at the top and a vertical stroke in the bottom right” which defines the complexity of a simple recognition system.
The neural network uses a large number of data sets to train a machine. It approaches machine learning to process and train a machine. In simpler words, NN can build an efficient machine by increasing the number of training sets. i.e. hundreds of training sets can make a good machine whereas thousands or millions of sets could build a better recognizer. Handwriting recognition is an excellent prototype problem for learning about neural networks in general so we’ll be talking about it to understand the working.
There are two types of artificial neurons:
1. Perceptron
2. Sigmoid neuron
The standard learning algorithm for neural networks is stochastic gradient descent.
Perceptrons
Perceptrons were found in the 1950s and 1960s by Frank Rosenblatt while the inspiration came from Warren McCulloch and Walter Pitts. The main neural model used in this modern world is the sigmoid neuron.
A perceptron takes few binary inputs giving a single binary output:
A perceptron takes few binary inputs giving a single binary output:
- Each input into the neuron has its own weight associated with it.
- As each input enters the nucleus (circle) it’s multiplied by its weight.
- The nucleus sums all these new input values which give us the activation.
- For n inputs and n weights – weights multiplied by input and summed
a = x1w1+x2w2+x3w3… +xnwn
- If the activation is greater than a threshold value – the neuron outputs a signal – (for example 1)
- If the activation is less than the threshold the neuron outputs zero.
- This is typically called a step function
0 if w⋅x+b≤0
1 if w⋅x+b>0
Inputs can be any kind of evidence or event, perceptron can weigh up different kinds of evidence in order to make decisions.
Similarly, we can have various layers, each having an input and giving out an output.
- The first column of perceptrons is called the first layer of perceptrons, making three very simple decisions, by weighing the input evidence.
- Each of those perceptions from layer two is decided by weighing up the results from the first layer output. In this way, a perceptron in the second layer can decide a more complex and more abstract level than the first layer. Hence even more complex decisions can be made by the perceptron in the third layer. In this way, a many-layer network of perceptrons can engage in sophisticated decision-making.
So far perceptrons have been described as a method for weighing evidence to make decisions. Another way perceptrons are used is to compute the elementary logical functions, functions such as AND, OR, and NAND. For example, suppose we have a perceptron with two inputs, each weight −2, and an overall bias of 3. Here’s our perception:
00 produces 1,
(−2)∗0 + (−2) ∗ 0 + 3
= 3(−2)∗0+(−2)∗0+3
=3 is positive.
11 produces 0,
(−2)∗1 + (−2)∗1 + 3
= −1(−2)∗1+(−2)∗1+3
=−1 is negative.
This NAND example shows us that we can use perceptrons to compute simple logical functions.
Suppose we have a perceptron with no inputs, then the weighted sum would always be zero, and so the perceptron would be:
output 1 if b > 0,
and 0 if b ≤ 0.
The computational universality of perceptrons is reassuring and disappointing, both at the same time.
It’s reassuring because it tells us that the networks of perceptrons can be as powerful as any other computing device.
But it is also disappointing because it makes it seem as though perceptrons are just a new type of NAND gate.
These learning algorithms we talked about, enable us to use artificial neurons in a way that is radically different from conventional logic gates. Our neural networks can simply learn to solve problems, sometimes problems where it would be extremely difficult to directly design a conventional circuit.
Sigmoid neurons
To see how learning works, we can make a small variation in the weight of the inputs (or bias) in the network. What we want is, for this small change in weight to cause only a small corresponding change in the output from the network.
Suppose that the machine was mistakenly classifying an image as an ‘8’ when it should have been a ‘9’. We need to figure out how to make a small change in the weights and biases so the network gets a little closer to classifying the image as a ‘9’. And then we will repeat this step of changing the weights and biases over and over to produce better and better output.
The problem we might face is that this isn’t what happens when our network contains perceptrons. Rather a small change in the weight or bias of any single perceptron in the network might cause the output of that perceptron to completely spin, say from 0 to 1, which may result in the behavior of the rest of the network to completely change in some very complicated way.
To overcome this problem there is another type of artificial neuron called a sigmoid neuron. They are similar to perceptrons, but more modified so that small changes in their weights and biases cause only a small change in their output.
The sigmoid neuron has inputs, but instead of 0 or 1, these can also take on any values between 0 and 1, for example, 0.538. Also just like perceptron, the sigmoid neuron has weight for each input, and an overall bias, But the output is not 0 or 1. rather, it is:
Σ(w⋅x+b) σ (w⋅x+b), where σ is called the sigmoid function which is :

More accurately, the output of a sigmoid neuron with input xn & weight wn and bias b is:
There is a resemblance between the perceptrons and sigmoid neurons:
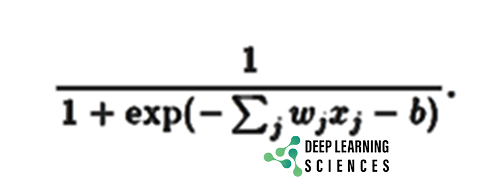
Like When z=w.x+bz=w.x+b is very negative, the behavior of a sigmoid neuron also closely approaches a perceptron. It’s only when w.x+bw.x+b is of modest size that there’s much deviance from the perceptron model.
The Architecture of Neural Networks(NN):
The leftmost layer is called the input layer, and the neurons in the layer are called input neurons. The rightmost or output layer contains the output neurons, or (in this case) a single output neuron. The middle layer is called the hidden layer, as the neurons in this layer aren’t inputs nor outputs (some networks have multiple hidden layers sometimes called multilayer perceptrons or MLPs).
We have discussed neural networks where the output from one layer is an input to the next layer, this is called a feedforward neural network. Though, there are other models of artificial neural networks (ANN) in which feedback loops are possible. These models are called recurrent neural networks.
A simple Network to classify handwritten digits: To recognize individual digits we will use a three-layer neural network:
Our training data for the network will consist of many 28 by 28-pixel images of handwritten digits that are scanned, and so the input layer contains 784=28×28 neurons. The input pixels are greyscaled, with a value of 0.0 representing white, a value of 1.0 representing black, and in between values representing gradually darkening shades of grey.
The second layer of the network is hidden. We denote the number of neurons in this layer by n, and we’ll experiment with different values for n.
The example illustrates a hidden layer, with n=15 neurons. The last/output layer of the network contains 10 neutrons. If the first neuron fires, i.e., has an output ≈1, then that will indicate that the network thinks the digit is a 0. If the second neuron fires then that will indicate that the network thinks the digit is a 1 and so on. Stay tuned with DLS.